2. Multiblock Framework

2.1. Motivation

A large class of problems can be solved by first decomposing the problem domain into a set of structured grids. For simplicity, each structured grid is often made rectangular, when it is called a block. These blocks may face one another or various parts of the outside world, and taken together comprise a multiblock computation.

There are two main types of multiblock computations – implicit and explicit. In an implicit computation, a global matrix, which represents the entire problem domain, is formed and solved. Implicit computations require a fast sparse matrix solver, and are typically used for steady-state problems. In an explicit computation, the solution proceeds locally, computing new values based on the values of nearby points. Explicit computations often have stability criteria, and are typically used for time-dependent problems.

The Charm++ multiblock framework allows you to write a parallel explicit multiblock program, in C or Fortran 90, by concentrating on what happens to a single block of the domain. Boundary condition housekeeping and “ghost cell” exchange are all handled transparently by the framework. Using the multiblock framework also allows you to take advantage of all the features of Charm++, including adaptive computation and communication overlap, run-time load balancing, performance monitoring and visualization, and checkpoint/restart, with no additional effort.

2.2. Introduction/Terminology

A block is a distorted rectangular grid that represents a portion of the problem domain. A volumetric cell in the grid is called a voxel. Each exterior side of a block is called a face. Each face may consist of several rectangular patches, which all abut the same block and experience the same boundary conditions.

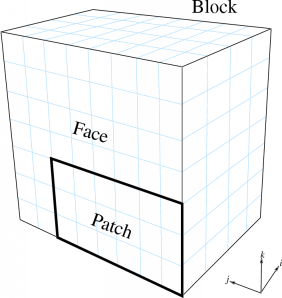
6 Terminology used by the framework.

For example, Figure 6 shows a 3D 4x8x7-voxel block, with a face and 6x3 patch indicated.

The computational domain is tiled with such blocks, which are required to be conformal – the voxels must match exactly. The blocks need not be the same size or orientation, however, as illustrated in the 2D domain of Figure 7.

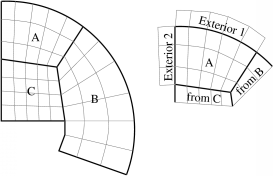
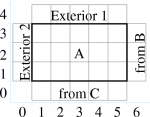
7 A 2D domain decomposed into three blocks: A (5x3), B (3x6), and C (5x4). Also shows the computation as seen from block A.

Figure 7 also shows the computation from the point of view of block A, which has two external boundary conditions (on the left and top sides) and two “internal” boundary conditions (on the right and bottom sides). During the computation, the external boundary conditions can be imposed independent of any other blocks; while the internal boundary conditions must be obtained from the other blocks.

To simplify the computation on the interior, these boundary conditions are typically written into special extra “ghost” (or dummy) cells around the outside of the real interior cells. The array indexing for these ghost cells is illustrated in Figure 8.

8 The ghost cells around a 5x3-voxel 2D block

The Multiblock framework manages all the boundary conditions – both internal and external. Internal boundary conditions are sent across processors, and require you to register the data “fields” you wish exchanged. External boundary conditions are not communicated, but require you to register a function to apply that boundary condition to your data. Either type of boundary condition can have arbitrary thickness.

Finally, the Multiblock framework manages nothing but boundary conditions. The rest of the computation, such as deciding on and implementing timestepping, stencils, numerics, and interpolation schemes are all left up to the user.

2.3. Input Files

The Multiblock framework reads, in parallel, a partitioned set of blocks from block input files. Each block consists of a file with extension “.mblk” for the interior data (grid coordinates and initial conditions) and “.bblk” for the boundary condition data (patches where boundaries should be applied).

These block files are generated with a separate, offline tool called “makemblock”, which is documented elsewhere.

2.4. Structure of a Multiblock Framework Program

A Multiblock framework program consists of several subroutines: init, driver, finalize, and external boundary condition subroutines.

init and finalize are called by the Multiblock framework only on the first processor – these routines typically do specialized I/O, startup and shutdown tasks.

A separate driver subroutine runs for each block, doing the main work of the program. Because there may be several blocks per processor, several driver routines may execute as threads simultaneously.

The boundary condition subroutines are called by the framework after a request from the driver.

subroutine init
     read configuration data
end subroutine

subroutine bc1
     apply first type of boundary condition
end subroutine bc1

subroutine bc2
     apply second type of boundary condition
end subroutine bc2

subroutine driver
     allocate and initialize the grid
     register boundary condition subroutines bc1 and bc2
     time loop
          apply external boundary conditions
          apply internal boundary conditions
          perform serial internal computation
     end time loop
end subroutine

subroutine finalize
      write results
end subroutine

2.5. Compilation and Execution

A Multiblock framework program is a Charm++ program, so you must begin by downloading the latest source version of Charm++ from https://charm.cs.illinois.edu. Build the source with ./build MBLOCK version or cd into the build directory, <version>/tmp, and type make MBLOCK. To compile a MULTIBLOCK program, pass the -language mblock (for C) or -language mblockf (for Fortran) option to charmc.

In a charm installation, see charm/<version>/pgms/charm++/mblock/ for example and test programs.

2.6. Preparing Input Files

The Multiblock framework reads its description of the problem domain from input “block” files, which are in a Multiblock-specific format. The files are named with the pattern prefixnumber.ext, where prefix is a arbitrary string prefix you choose, number is the number of this block (virtual processor), and ext is either “mblk”, which contains binary data with the block coordinates, or “bblk”, which contains ASCII data with the block’s boundary conditions.

You generate these Multiblock input files using a tool called makemblock, which can be found in charm/<version>/pgms/charm++/makemblock. makemblock can read a description of the problem domain generated by the structured meshing program Gridgen (from Pointwise) in .grd and .inp format; or read a binary .msh format. makemblock divides this input domain into the number of blocks you specify, then writes out .mblk and .bblk files.

For example, to divide the single binary mesh “in1.msh” into 20 pieces “out00001.[mb]blk”..“out00020.[mb]blk”, you’d use

$ makemblock in1.msh 20 out

You would then run this mesh using 20 virtual processors.

2.7. Multiblock Framework API Reference

The Multiblock framework is accessed from a program via a set of routines. These routines are available in both C and Fortran90 versions. The C versions are all functions, and always return an error code of MBLK_SUCCESS or MBLK_FAILURE. The Fortran90 versions are all subroutines, and take an extra integer parameter “err” which will be set to MBLK_SUCCESS or MBLK_FAILURE.

2.7.1. Initialization

All these methods should be called from the init function by the user. The values passed to these functions are typically read from a configuration file or computed from command-line parameters.

int MBLK_Set_prefix(const char *prefix);

subroutine MBLK_Set_prefix(prefix,err)
character*, intent(in)::prefix
integer, intent(out)::err

This function is called to set the block filename prefix. For example, if the input block files are named “gridX00001.mblk” and “gridX00002.mblk”, the prefix is the string “gridX”.

int MBLK_Set_nblocks(const int n);

subroutine MBLK_Set_nblocks(n,err)
integer, intent(in)::n
integer, intent(out)::err

This call is made to set the number of partitioned blocks to be used. Each block is read from an input file and a separate driver is spawned for each. The number of blocks determines the available parallelism, so be sure to have at least as many blocks as processors. We recommend using several times more blocks than processors, to ease load balancing and allow adaptive overlap of computation and communication.

Be sure to set the number of blocks equal to the number of virtual processors (+vp command-line option).

int MBLK_Set_dim(const int n);

subroutine MBLK_Set_dim(n, err)
integer, intent(in)::n
integer, intent(out)::err

This call is made to set the number of spatial dimensions. Only three dimensional computations are currently supported.

2.7.2. Utility

int MBLK_Get_nblocks(int* n);

subroutine MBLK_Get_nblocks(n,err)
integer,intent(out)::n
integer,intent(out)::err

Get the total number of blocks in the current computation. Can only be called from the driver routine.

int MBLK_Get_myblock(int* m);

subroutine MBLK_Get_myblock(m,err)
integer,intent(out)::m
integer,intent(out)::err

Get the id of the current block, an integer from 0 to the number of blocks minus one. Can only be called from the driver routine.

int MBLK_Get_blocksize(int* dims);

subroutine MBLK_Get_blocksize(dimsm,err)
integer,intent(out)::dims(3)
integer,intent(out)::err

Get the interior dimensions of the current block, in voxels. The size of the array dims should be 3, and will be filled with the \(i\), \(j\), and \(k\) dimensions of the block. Can only be called from the driver routine.

int MBLK_Get_nodelocs(const int* nodedim,double *nodelocs);

subroutine MBLK_Get_blocksize(nodedim,nodelocs,err)
integer,intent(in)::nodedims(3)
double precision,intent(out)::nodedims(3,nodedims(0),nodedims(1),nodedims(2))
integer,intent(out)::err

Get the \((x,y,z)\) locations of the nodes of the current block. The 3-array nodedim should be the number of nodes you expect, which must be exactly one more than the number of interior voxels.

9 The C node and voxel \((i,j,k)\) numbering for a 2 x 2 voxel block. For the fortran numbering, add 1 to all indices. Ghost voxels are omitted.

You cannot obtain the locations of ghost nodes via this routine. To get the locations of ghost nodes, create a node-centered field containing the node locations and do an update field. Can only be called from the driver routine.

double MBLK_Timer(void);

function double precision :: MBLK_Timer()

Return the current wall clock time, in seconds. Resolution is machine-dependent, but is at worst 10ms.

void MBLK_Print_block(void);

subroutine MBLK_Print_block()

Print a debugging representation of the framework’s information about the current block.

void MBLK_Print(const char *str);

subroutine MBLK_Print(str)
character*, intent(in) :: str

Print the given string, prepended by the block id if called from the driver. Works on all machines, unlike printf or print *, which may not work on all parallel machines.

2.7.3. Internal Boundary Conditions and Block Fields

The Multiblock framework handles the exchange of boundary values between neighboring blocks. The basic mechanism to do this exchange is the field – numeric data items associated with each cell of a block. These items must be arranged in a regular 3D grid, but otherwise we make no assumptions about the meaning of a field.

You create a field once, with MBLK_Create_Field, then pass the resulting field ID to MBLK_Update_Field (which does the overlapping block communication) and/or MBLK_Reduce_Field (which applies a reduction over block values).

int MBLK_Create_Field(int *dimensions,int isVoxel,const int
base_type,const int vec_len,const int offset,const int dist, int
*fid);

subroutine MBLK_Create_Field(dimensions, isVoxel,base_type, vec_len, offset, dist, err)
integer, intent(in) :: dimensions, isVoxel, base_type, vec_len, offset, dist
integer, intent(out) :: fid, err

Creates and returns a Multiblock field ID, which can be passed to MBLK_Update_Field and MBLK_Reduce_Field. Can only be called from driver().

dimensions describes the size of the array the field is in as an array of size 3, giving the \(i\), \(j\), and \(k\) sizes. The size should include the ghost regions – i.e., pass the actual allocated size of the array. isVoxel describes whether the data item is to be associated with a voxel (1, a volume-centered value) or the nodes (0, a node-centered value). base_type describes the type of each data item, one of:

• MBLK_BYTE – unsigned char, INTEGER*1, or CHARACTER*1

• MBLK_INT – int or INTEGER*4

• MBLK_REAL – float or REAL*4

• MBLK_DOUBLE – double, DOUBLE PRECISION, or REAL*8

vec_len describes the number of data items associated with each cell, an integer at least 1.

offset is the byte offset from the start of the array to the first interior cell’s data items, a non-negative integer. This can be calculated using the offsetof() function, normally with offsetof(array(1,1,1), array(interiorX,interiorY,interiorZ)). Be sure to skip over any ghost regions.

dist is the byte offset from the first cell’s data items to the second, a positive integer (normally the size of the data items). This can also be calculated using offsetof(); normally with offsetof(array(1,1,1), array(2,1,1)).

fid is the identifier for the field that is created by the function.

In the example below, we register a single double-precision value with each voxel. The ghost region is 2 cells deep along all sides.

!In Fortran
double precision, allocatable :: voxData(:,:,:)
integer :: size(3), ni,nj,nk
integer :: fid, err

!Find the dimensions of the grid interior
MBLK_Get_blocksize(size,err);

!Add ghost region width to the interior dimensions
size=size+4;  ! 4 because of the 2-deep region on both sides

!Allocate and initialize the grid
allocate(voxData(size(1),size(2),size(3)))
voxData=0.0

!Create a field for voxData
call MBLK_Create_field(&
       &size,1, MBLK_DOUBLE,3,&
       &offsetof(grid(1,1,1),grid(3,3,3)),&
       &offsetof(grid(1,1,1),grid(2,1,1)),fid,err)

This example uses the Fortran-only helper routine offsetof, which returns the offset in bytes of memory between its two given variables. C users can use the built-in sizeof keyword or pointer arithmetic to achieve the same result.

void MBLK_Update_field(const int fid,int ghostwidth, void *grid);

subroutine MBLK_Update_field(fid,ghostwidth, grid,err)
integer, intent(in) :: fid, ghostwidth
integer,intent(out) :: err
varies, intent(inout) :: grid

Update the values in the ghost regions specified when the field was created. This call sends this block’s interior region out, and receives this block’s boundary region from adjoining blocks.

ghostwidth controls the thickness of the ghost region. To exchange only one cell on the boundary, pass 1. To exchange two cells, pass 2. To include diagonal regions, make the ghost width negative. A ghost width of zero would communicate no data.

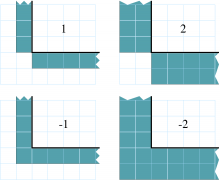
10 The 2D ghost cells communicated for various ghost widths. The heavy line is the block interior boundary – this is the lower left portion of the block.

MBLK_Update_field can only be called from the driver, and to be useful, must be called from every block’s driver routine.

MBLK_Update_field blocks until the field has been updated. After this routine returns, the given field will updated. If the update was successful MBLK_SUCCESS is returned, otherwise MBLK_FAILURE is returned in case of error.

void MBLK_Iupdate_field(const int fid,int ghostwidth, void *ingrid, void* outgrid);

subroutine MBLK_Iupdate_field(fid,ghostwidth, ingrid, outgrid,err)
integer, intent(in) :: fid, ghostwidth
integer,intent(out) :: err
varies,intent(in) :: ingrid
varies,intent(out) :: outgrid

Update the values in the ghost regions which were specified when the field was created. For the example above the ghost regions will be updated once for each step in the time loop.

MBLK_Iupdate_field can only be called from the driver, and to be useful, must be called from every block’s driver routine.

MBLK_Iupdate_field is a non blocking call similar to MPI_Irecv. After the routine returns the update may not yet be complete and the outgrid may be in an inconsistent state. Before using the values, the status of the update must be checked using MBLK_Test_update or MBLK_Wait_update.

There can be only one outstanding Iupdate call in progress at any time.

int MBLK_Test_update(int *status);

subroutine MBLK_Test_update(status,err)
integer, intent(out) :: status,err

MBLK_Test_update is a call that is used in association with MBLK_Iupdate_field from the driver subroutine. It tests whether the preceding Iupdate has completed or not. status is returned as MBLK_DONE if the update was completed or MBLK_NOTDONE if the update is still pending. Rather than looping if the update is still pending, call MBLK_Wait_update to relinquish the CPU.

void MBLK_Wait_update(void);

subroutine MBLK_Wait_update()

MBLK_Wait_update call is a blocking call and is used in association with MBLK_Iupdate_field call. It blocks until the update is completed.

void MBLK_Reduce_field(int fid,void *grid, void *out,int op);

subroutine MBLK_Reduce_field(fid,grid,outVal,op)
integer, intent(in) :: fid,op
varies, intent(in) :: grid
varies, intent(out) :: outVal

Combine a field from each block, according to op, across all blocks. Only the interior values of the field will be combined, not the ghost cells. After Reduce_Field returns, all blocks will have identical values in outVal, which must be vec_len copies of base_type.

May only be called from the driver, and to complete, must be called from every chunk’s driver routine.

op must be one of:

• MBLK_SUM – each element of outVal will be the sum of the corresponding fields of all blocks

• MBLK_MIN – each element of outVal will be the smallest value among the corresponding field of all blocks

• MBLK_MAX – each element of outVal will be the largest value among the corresponding field of all blocks

void MBLK_Reduce(int fid,void *inVal,void *outVal,int op);

subroutine MBLK_Reduce(fid,inVal,outVal,op)
integer, intent(in) :: fid,op
varies, intent(in) :: inVal
varies, intent(out) :: outVal

Combine a field from each block, acoording to op, across all blocks. fid is only used for base_type and vec_len – offset and dist are not used. After this call returns, all blocks will have identical values in outVal. op has the same values and meaning as MBLK_Reduce_Field. May only be called from the driver, and to complete, must be called from every block’s driver routine.

2.7.4. External Boundary Conditions

Most problems include some sort of boundary conditions. These conditions are normally applied in the ghost cells surrounding the actual computational domain. Examples of boundary conditions are imposed values, reflection walls, symmetry planes, inlets, and exits.

The Multiblock framework keeps track of where boundary conditions are to be applied. You register a subroutine that the framework will call to apply each type of external boundary condition.

int MBLK_Register_bc(const int bcnum, int ghostWidth, const MBLK_BcFn bcfn);

subroutine MBLK_Register_bc(bcnum, ghostwidth, bcfn, err)
integer,intent(in) :: bcnum, ghostWidth
integer,intent(out) :: err
subroutine :: bcfn

This call is used to bind an external boundary condition subroutine, written by you, to a boundary condition number. MBLK_Register_bc should only be called from the driver.

• bcnum – The boundary condition number to be associated with the function.

• ghostWidth – The width of the ghost cells where this boundary condition is to be applied.

• bcfn – The user subroutine to be called to apply this boundry condition.

When you ask the framework to apply boundary conditions, it will call this routine. The routine should be declared like:

!In Fortran
subroutine applyMyBC(param1,param2,start,end)
varies :: param1, param2
integer :: start(3), end(3)
end subroutine

/* In C */
void applyMyBC(void *param1,void *param2,int *start,int *end);

param1 and param2 are not used by the framework – they are passed in unmodified from MBLK_Apply_bc and MBLK_Apply_bc_all. param1 and param2 typically contain the block data and dimensions.

start and end are 3-element arrays that give the \(i\),\(j\), \(k\) block locations where the boundary condition is to be applied. They are both inclusive and both relative to the block interior – you must shift them over your ghost cells. The C versions are 0-based (the first index is zero), while the Fortran versions are 1-based (the first index is one).

For example, a Fortran subroutine to apply the constant value 1.0 across the boundary, with a 2-deep ghost region, would be:

!In Fortran
subroutine applyMyBC(grid,size,start,end)
  integer :: size(3), i,j,k
  double precision :: grid(size(1),size(2),size(3))
  integer :: start(3), end(3)
  start=start+2 ! Back up over ghost region
  end=end+2
  do i=start(1),end(1)
   do j=start(2),end(2)
     do k=start(3),end(3)
       grid(i,j,k)=1.0
     end do
   end do
  end do

end subroutine

int MBLK_Apply_bc(const int bcnum, void *param1,void *param2);

subroutine MBLK_Apply_bc(bcnum, param1,param2,err)
integer,intent(in)::bcnum
varies,intent(inout)::param1
varies,intent(inout)::param2
integer,intent(out)::err

MBLK_Apply_bc call is made to apply all boundary condition functions of type bcnum to the block. param1 and param2 are passed unmodified to the boundary condition function.

int MBLK_Apply_bc_all(void* param1, void* param2);

subroutine MBLK_Apply_bc_all(param1,param2, err)
integer,intent(out)::err
varies,intent(inout)::param1
varies,intent(inout)::param2

This call is same as MBLK_Apply_bc except it applies all external boundary conditions to the block.

2.7.5. Migration

The Charm++ runtime system includes automated, runtime load balancing, which will automatically monitor the performance of your parallel program. If needed, the load balancer can “migrate” mesh chunks from heavily-loaded processors to more lightly-loaded processors, improving the load balance and speeding up the program. For this to be useful, pass the +vpN argument with a larger number of blocks N than processors Because this is somewhat involved, you may refrain from calling MBLK_Migrate and migration will never take place.

The runtime system can automatically move your thread stack to the new processor, but you must write a PUP function to move any global or heap-allocated data to the new processor. (Global data is declared at file scope or static in C and COMMON in Fortran77. Heap allocated data comes from C malloc, C++ new, or Fortran90 ALLOCATE.) A PUP (Pack/UnPack) function performs both packing (converting heap data into a message) and unpacking (converting a message back into heap data). All your global and heap data must be collected into a single block (struct in C, user-defined TYPE in Fortran) so the PUP function can access it all.

Your PUP function will be passed a pointer to your heap data block and a special handle called a “pupper”, which contains the network message to be sent. Your PUP function returns a pointer to your heap data block. In a PUP function, you pass all your heap data to routines named pup_type, where type is either a basic type (such as int, char, float, or double) or an array type (as before, but with a “s” suffix). Depending on the direction of packing, the pupper will either read from or write to the values you pass – normally, you shouldn’t even know which. The only time you need to know the direction is when you are leaving a processor or just arriving. Correspondingly, the pupper passed to you may be deleting (indicating that you are leaving the processor, and should delete your heap storage after packing), unpacking (indicating you’ve just arrived on a processor, and should allocate your heap storage before unpacking), or neither (indicating the system is merely sizing a buffer, or checkpointing your values).

PUP functions are much easier to write than explain – a simple C heap block and the corresponding PUP function is:

typedef struct {
  int n1; /*Length of first array below*/
  int n2; /*Length of second array below*/
  double *arr1; /*Some doubles, allocated on the heap*/
  int *arr2; /*Some ints, allocated on the heap*/
} my_block;

my_block *pup_my_block(pup_er p,my_block *m)
{
  if (pup_isUnpacking(p)) m=malloc(sizeof(my_block));
  pup_int(p, &m->n1);
  pup_int(p, &m->n2);
  if (pup_isUnpacking(p)) {
    m->arr1=malloc(m->n1*sizeof(double));
    m->arr2=malloc(m->n2*sizeof(int));
  }
  pup_doubles(p,m->arr1,m->n1);
  pup_ints(p,m->arr2,m->n2);
  if (pup_isDeleting(p)) {
    free(m->arr1);
    free(m->arr2);
    free(m);
  }
  return m;
}

This single PUP function can be used to copy the my_block data into a message buffer and free the old heap storage (deleting pupper), allocate storage on the new processor and copy the message data back (unpacking pupper), or save the heap data for debugging or checkpointing.

A Fortran TYPE block and corresponding PUP routine is as follows:

MODULE my_block_mod
  TYPE my_block
    INTEGER :: n1,n2x,n2y
    REAL*8, POINTER, DIMENSION(:) :: arr1
    INTEGER, POINTER, DIMENSION(:,:) :: arr2
  END TYPE
END MODULE

SUBROUTINE pup_my_block(p,m)
  IMPLICIT NONE
  USE my_block_mod
  USE pupmod
  INTEGER :: p
  TYPE(my_block) :: m
  call pup_int(p,m%n1)
  call pup_int(p,m%n2x)
  call pup_int(p,m%n2y)
  IF (pup_isUnpacking(p)) THEN
    ALLOCATE(m%arr1(m%n1))
    ALLOCATE(m%arr2(m%n2x,m%n2y))
  END IF
  call pup_doubles(p,m%arr1,m%n1)
  call pup_ints(p,m%arr2,m%n2x*m%n2y)
  IF (pup_isDeleting(p)) THEN
    DEALLOCATE(m%arr1)
    DEALLOCATE(m%arr2)
  END IF
END SUBROUTINE

int MBLK_Register(void *block, MBLK_PupFn pup_ud, int* rid)

subroutine MBLK_Register(block,pup_ud, rid)
integer, intent(out)::rid
TYPE(varies), POINTER :: block
SUBROUTINE :: pup_ud

Associates the given data block and PUP function. Returns a block ID, which can be passed to MBLK_Get_registered later. Can only be called from driver. It returns MBLK_SUCESS if the call was successful and MBLK_FAILURE in case of error. For the declarations above, you call MBLK_Register as:

/*C/C++ driver() function*/
int myId, err;
my_block *m=malloc(sizeof(my_block));
err =MBLK_Register(m,(MBLK_PupFn)pup_my_block,&rid);

!- Fortran driver subroutine
use my_block_mod
interface
  subroutine pup_my_block(p,m)
    use my_block_mod
    INTEGER :: p
    TYPE(my_block) :: m
  end subroutine
end interface
TYPE(my_block) :: m
INTEGER :: myId,err
MBLK_Register(m,pup_my_block,myId,err)

Note that Fortran blocks must be allocated on the stack in driver, while C/C++ blocks may be allocated on the heap.

void MBLK_Migrate()

subroutine MBLK_Migrate()

Informs the load balancing system that you are ready to be migrated, if needed. If the system decides to migrate you, the PUP function passed to MBLK_Register will be called with a sizing pupper, then a packing and deleting pupper. Your stack (and pupped data) will then be sent to the destination machine, where your PUP function will be called with an unpacking pupper. MBLK_Migrate will then return, whereupon you should call MBLK_Get_registered to get your unpacked data block. Can only be called from the driver.

int MBLK_Get_Userdata(int n, void** block)

Return your unpacked userdata after migration – that is, the return value of the unpacking call – to your PUP function. Takes the userdata ID returned by MBLK_Register. Can be called from the driver at any time.

Since Fortran blocks are always allocated on the stack, the system migrates them to the same location on the new processor, so no Get_Registered call is needed from Fortran.